Ice I_h

Ice I_h is the hexagonal crystal form of ordinary ice, or frozen water.^[1] Virtually all ice in the biosphere is ice I_h, with the exception only of a small amount of ice I_c which is occasionally present in the upper atmosphere. Ice I_h exhibits many peculiar properties which are relevant to the existence of life and regulation of global climate.^[2]

Ice I_h is stable down to −200 °C (73 K; −328 °F) and can exist at pressures up to 0.2 GPa. The crystal structure is characterized by hexagonal symmetry and near tetrahedral bonding angles.

Physical properties

Ice I_h has a density less than liquid water, of 0.917 g/cm³, due to the extremely low density of its crystal lattice. The density of ice I_h increases with decreasing temperature (density of ice at -180 °C is 0.9340 g/cm³).

The latent heat of melting is 5987 J/mol, and its latent heat of sublimation is 50911 J/mol. The high latent heat of sublimation is principally indicative of the strength of the hydrogen bonds in the crystal lattice. The latent heat of melting is much smaller partly because water near 0 °C is very strongly H-bonded already.

The refractive index of ice I_h is 1.31.

Crystal structure

The accepted crystal structure of ordinary ice was first proposed by Linus Pauling in 1935. The structure of ice I_h is roughly one of crinkled planes composed of tessellating hexagonal rings, with an oxygen atom on each vertex, and the edges of the rings formed by hydrogen bonds. The planes alternate in an ABAB pattern, with B planes being reflections of the A planes along the same axes as the planes themselves. The distance between oxygen atoms along each bond is about 275 pm and is the same between any two bonded oxygen atoms in the lattice. The angle between bonds in the crystal lattice is very close to the tetrahedral angle of 109.5° which is also quite close to the angle between hydrogen atoms in the water molecule (in the gas phase), which is 105°. This tetrahedral bonding angle of the water molecule essentially accounts for the unusually low density of the crystal lattice -- it is beneficial for the lattice to be arranged with tetrahedral angles even though there is an energy penalty in the increased volume of the crystal lattice. As a result, the large hexagonal rings leave almost enough room for another water molecule to exist inside. This gives naturally occurring ice its unique property of being less dense than its liquid form. The tetrahedral-angled hydrogen-bonded hexagonal rings are also the mechanism which causes liquid water to be most dense at 4 °C. Close to 0 °C, tiny hexagonal ice I_h-like lattices form in liquid water, with greater frequency closer to 0 °C. This effect decreases the density of the water, causing it to be most dense at 4 °C when the structures form infrequently.

Proton disorder

The protons (hydrogen atoms) in the crystal lattice lie very nearly along the hydrogen bonds, and in such a way that each water molecule is preserved. This means that each oxygen atom in the lattice has two protons adjacent to it, at about 101 pm along the 275 pm length of the bond. The crystal lattice allows a substantial amount of disorder in the positions of the protons frozen into the structure as it cools to absolute zero. As a result, the crystal structure contains some residual entropy inherent to the lattice and determined by the number of possible configurations of proton positions which can be formed while still maintaining the requirement for each oxygen atom to have only two protons in closest proximity, and each H-bond joining two oxygen atoms having only one proton. This residual entropy S₀ is equal to 3.5 J mol⁻¹ K⁻¹. There are various ways of approximating this number from first principles. Assuming a given N water molecules each has 6 possible arrangements this yields 6^N possible combinations. Given random orientations of molecules, a given bond will have only a ½ chance that it has exactly one proton, or in other words, each molecule has a ¼ chance that its protons lie on bonds containing exactly one proton, leaving a total number of 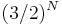possible valid combinations. Using Boltzmann's principle, we find that 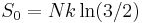, where is the Boltzmann constant, which yields a value of 3.37 J mol⁻¹ K⁻¹, a value very close to the measured value. More complex methods can be employed to better approximate the exact number of possible configurations, and achieve results closer to measured values.

By contrast, the structure of ice II is very proton-ordered, which helps to explain the entropy change of 3.22 J/mol when the crystal structure changes to that of ice II. Also, ice XI, an orthorhombic, proton-ordered form of ice I_h, is considered the most stable form.

Notes

1. ^ Norman Anderson. The Many Phases of Ice. Iowa State University. http://atom.me.gatech.edu/zhut/Courses/Courses_HarvardCollection/caiwei/phasesofice.pdf. 
2. ^ For a description of these properties, see Ice, which deals primarily with Ice I_h.

See also

• Ice for other crystalline form of ice

References

• N. H. Fletcher, The Chemical Physics of Ice, Cambridge UP (1970) ISBN 0-521-07597-1
• Victor F. Petrenko and Robert W. Whitworth, Physics of Ice, Oxford UP (1999) ISBN 0-19-851894-3
• Chaplin, Martin (2007-11-11). "Hexagonal ice structure". Water Structure and Science. http://www.lsbu.ac.uk/water/ice1h.html. Retrieved 2008-01-02.